四种DRL算法的异同

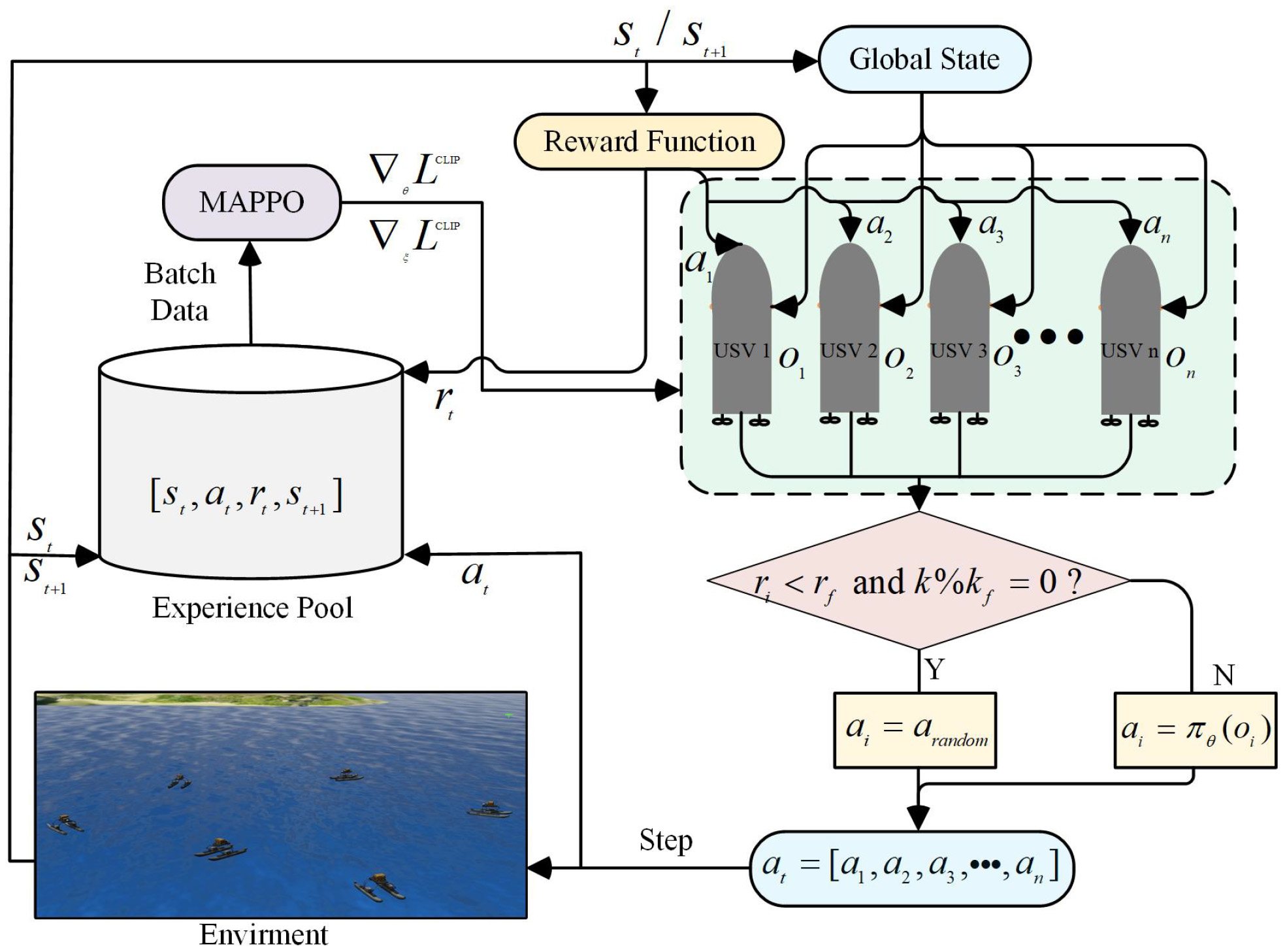
MADDPG^[1]、MATD3、MAPPO^[2]与PMPO的异同

MADDPG、MATD3、MAPPO与PMPO四种算法都是“多智能体强化学习”的不同做法，可以把它们理解成为同一个目标下的四种“学习风格”。

一、共同目标

举一个简单的例子 几个小机器人在一起搬箱子，每个机器人都能看到一部分环境，却不知道别人怎么想，它们必须一起完成任务，但每个机器人都在“自私地”学自己的策略，因此整个环境总是在变，学习容易不稳定。

这四个算法都是用来解决这个核心问题：多智能体一起学习，但环境因为大家同时变化而变得很难学。

四者的共同点有：

1. 都属于多智能体强化学习，适用于多个智能体共同完成任务；
2. 都采用集中训练、分散执行的方式。训练时共享一些信息，执行时各自独立；
3. 都试图让学习过程稳定，避免“你变我变大家都变导致学不会”的情况

二、四个算法的直观区别

1. MADDPG

• 比喻：MADDPG就像每个学生都用自己的笔记(actor)，但考试时老师(critic)会告诉每个学生“我看到了全班人的答案，你这个答案好不好”，所以其比单独学习更稳定；
• 技术特点：是DDPG^[3]的多智能体版本，适合连续动作问题，比如机器人控制；
• 优点：容易理解，容易实现，比单智能体更稳定；
• 缺点：DDPG本身不太稳定，训练容易受超参数影响。

2. MATD3

• 比喻：比MADDPG更聪明的学生。他知道“老师可能偏心，把分数打高了”，于是引入两个老师（双Q值）同时评分，让分数更真实，从而学习更稳；
• 技术特点：是TD3^[4]的多智能体版本，因此比MADDPG大幅提升稳定性；
• 优点：比MADDPG更稳，更不容易学炸；
• 缺点：仍然属于确定性策略，探索不如随机策略。

3. MAPPO

• 比喻：这群学生的学习方式变了，不是去猜正确答案，而是“学习一套概率分布”，让自己的行为更有弹性，并利用“概率裁剪”（防止更新太猛）保持稳定；
• 技术特点：基于PPO^[5]的多智能体方法，现在非常流行；
• 优点：非常稳定，特别适合大规模智能体，比如多人对抗游戏、交通调度等；
• 缺点：在某些高精度连续控制任务的样本效率不如TD3/MATD3。

4. PMPO

• 比喻：这群学生不光学习自己的策略，它们还学习“大家之间如何协作的概率关系”，有点像研究团队合作模式的学生，把协作结构建模得更细；
• 技术特点：基于策略梯度，重点在于“建模智能体之间的协作概率结构”；
• 优点：更强的协同能力，更适合复杂任务；
• 缺点：计算复杂度比较高，不如MAPPO那样广泛使用。

三、总结

按学习方式分类：

• 确定性策略方法：MADDPG和MATD3
• 随机策略方法：MAPPO和PMPO

按稳定性：

• 最稳定：MATD3和MAPPO
• 较不稳定：MADDPG
• 稳定但复杂度高：PMPO

MADDPG：多智能体版 DDPG，简单但不够稳。

MATD3：加强版 MADDPG，更稳定。

MAPPO：多智能体 PPO，最稳定使用最广。

PMPO：建模协作结构更强，但更复杂。

相对应的应用背景：

• 机器人或物理控制类：MATD3。
• 游戏对抗、多智能体协作：MAPPO。
• 新颖的研究、强化智能体协作结构：PMPO。
• 简单跑通一个demo：MADDPG 或 MAPPO

1. Lowe R, Wu Y I, Tamar A, et al. Multi-agent actor-critic for mixed cooperative-competitive environments[J]. Advances in neural information processing systems, 2017, 30.
2. Yu C, Velu A, Vinitsky E, et al. The Surprising Effectiveness of PPO in Cooperative Multi-Agent Games[C]//Thirty-sixth Conference on Neural Information Processing Systems Datasets and Benchmarks Track.
3. Lillicrap T P, Hunt J J, Pritzel A, et al. Continuous control with deep reinforcement learning[J]. arXiv preprint arXiv:1509.02971, 2015.
4. Fujimoto S, Hoof H, Meger D. Addressing function approximation error in actor-critic methods[C]//International conference on machine learning. PMLR, 2018: 1587-1596.
5. Schulman J, Wolski F, Dhariwal P, et al. Proximal policy optimization algorithms[J]. arXiv preprint arXiv:1707.06347, 2017.