台风过程的大气-海洋-海浪耦合与卫星数据同化模拟
摘要
对于台风多发海域，准确模拟出台风过程风场、波浪场和流场是至关重要的。本文采用 MCT 耦合器将中尺度大气模型 WRF、非结构化网络海洋模型 FVCOM 及非结构化网格波浪模型 SWAN 进行耦合，并在计算过程中利用 WRF 大气模式的资料同化模块 WRFDA 对风场进行卫星资料同化，即建立大气-海洋-海浪实时耦合模型与卫星数据同化的联合运用模型（WRF-FVCOM-SWAN-ASSIMILATION 模型，简称 W-F-S-A 模型），对海南岛附近海域台风过程进行模拟，进一步获得了设计要素。论文的主要工作和结论如下：
在通过 MCT 耦合器实现 WRF-FVCOM-SWAN 模型耦合的基础上，通过 FVCOM 模式和 SWAN 模式的热启动，成功建立了 WRF-FVCOM-SWAN-ASSIMILATION（W-F-S-A）耦合同化数学模型（以下简称 W-F-S-A 耦合同化模型）。
分别基于纯 WRF 模型驱动、纯耦合模型、W-F-S-A 耦合同化模型对台风风场路径和强度、海表温度场、波浪场模拟结果进行了比较，结果表明，W-F-S-A 耦合同化模型模拟结果与实测数据偏差最小。
对 1999 - 2018 共 20 年间经过海南岛附近海域的 70 场台风进行了 W-F-S-A 耦合同化模拟，得到了台风过程风场、海表流场、海表温度场和波浪场模拟结果。
基于 20 年台风过程风、浪模拟结果，获得了单一变量和联合分布的不同重现期设计要素。
关键词： 大气-海洋-海浪耦合模型；连续同化；台风；频率分析；联合分布
绪论
研究目的和意义
台风具有极强的破坏性，对于建筑物、沿海生态系统、电力设施都具有较大的危害。而且从台风发生的空间分布来看，西北太平洋是全球台风发生频率最高的区域，约占全球总数的 1/3。我刚频率西北太平洋，是全球范围内受台风影响最大的国家之一，年平均有 9.3 个台风影响我国，居世界之首。近年来，南海作为我国重要战略区域的地位日趋明显，获得南海海域的海洋环境设计要素对于南海海上工程的建设十分关键。获得合理设计参数需要对台风过程的风场、流场以及波浪场进行模拟。因此，如何合理准确地模拟台风过程中的风、浪、流过程，具有十分重要的意义，成为本文研究的主要内容。
国内外主要研究进展
台风过程风、浪、流的特征
台风风场特征
台风风场的平面结构可以简单分成两部分，其中心区域为台风眼区，是一个低压区，风速很弱；台风眼区外的空气向台风眼汇合，在北半球气流呈逆时针方向旋转，且产生大风区。另外，由于在北半球，空气质点受到的科氏力与径向速度垂直，使得台风的运动呈右偏性。
台风过程中海洋的响应特征
台风过程中海洋的响应特征体现在两方面，一方面是对海表流场的影响，另一方面是对海表温度场的影响。
-
海表流场： 台风过境时，受风应力作用，海表会形成旋转流场。台风过境时，海表往往会形成逆时针旋转流场，流场中心位于台风中心的右后方，具有一定的滞后性。且流场具有明显的右偏性，台风移动路径右侧的流速大于左侧。
-
海表温度场： 台风过境时，会引起海表较大幅度的降温，最大降温幅度受台风强度、海洋结构的影响。且温度场受风场制约呈不对称分布，具有明显的右偏性，最大降温区位于台风移动路径的右侧。
台风过程中海浪的响应特征
台风过程中，巨大的风应力会产生强烈的风浪，风浪与远处传来的涌浪叠加，构成了台风浪，台风浪的时空分布特征主要受台风风场制约，同时也受岛屿效应、海底地形以及潮流的影响。台风过境时，海表会形成旋转波浪场，呈椭圆形分布，且波浪场受风场制约呈不对称分布，具有明显的右偏性，台风移动路径右侧的有效波高大于左侧。
台风过程数值模拟
台风过程风场数值模拟
近年来台风模拟的发展较为迅速，从早期的客观分析法，到经验模型法，再至现在常用的数值模拟法，对于台风模拟的精度提升和风场刻画日趋完善。
客观分析法： 风场计算最传统的方法，其原理是将气象站的观测资料在地形网格上进行插值，从而实现风场数据的扩充，同时利用相关的约束条件与物理方程对风场数据进行修正，使数据满足动力平衡条件。但修正后的数据仍具有观测资料本身具有的不连续性、风速局限性、不稳定性等特点，同时还有观测的偶然性误差。
经验模型法： 使用相关的台风模型取代了物理约束方程，但是其本质上并没有改善实测数据质量和数量的不足，并且台风模型多为轴对称模型，对于实现高精度模拟和台风复杂风场的刻画还是有一定难度。
数值模拟法： 随着计算机技术的快速发展，其成为新的研究方向，同时人们也要通过寻求更精确的风场资料、研究更完备的台风模型去改善台风模拟结果。对于风场资料的获取也从最初的仪器观测资料，发展到雷达资料，再到卫星数据资料，目前已发展至卫星资料再分析数据，这从源头上提高了风场模拟的精度。近年来，数值模拟方法不断发展，中尺度大气模式逐渐成为主流。
台风过程流场和温度场数值模拟
台风对海洋的作用主要体现在海表流场和海表温度场这两方面，这两者的模拟主要通过海洋模式实现，目前海洋模式已发展到三维模拟，国内外普遍采用的模式主要由 ECOM、ROMS、POM、和 FVCOM 等。其中前三种模型多采用结构化网格，这对于实际岸线的刻画是不利的。FVCOM 海洋模型采用三角形网格，即非结构化网格，可模拟复杂岸线对流场和温度场的影响，其能较好地刻画出流场、温度场的右偏性、以及流场的滞后性等特点。
台风过程波浪场数值模拟
波浪研究一直是国内外海洋动力学研究的热门话题，对于波浪参数与波浪传播过程的模拟计算，目前主流的方法是通过数学模型求解波浪在传播过程中的折射、绕射效应以及浅水变形，数学模型原理主要分为经典的射线理论、缓坡方程、Boussinesq 方程和波作用谱平衡方程。在上世纪八十年代后期，研究者开始利用波作用谱方程作为数学模型模拟波浪。目前已经发展至第三代海浪模式，主要包括 WAM、WAVEWATCH III、SWAN 等。近年来的波浪模拟普遍采用了风场驱动海浪模式的计算方法进行数值模拟，在一定程度上提高了模拟效果。研究发现，在复杂地形中，利用嵌套模式是更为科学准确的。
耦合模式对台风的数值模拟
台风与海洋之间存在强烈的热量交换，台风过境时会导致海表温度下降，且台风强度越大，海表温度降低的幅度越大。相应地，海表温度降低会减少供给台风的潜热通量、感热通量和水汽通量，导致台风强度减弱。另一方面，台风在海表产生的近惯性流也会导致混合层温度持续降低，从而减弱台风强度。因此为了更真实地模拟出台风过程的风场、流场和温度场，需要建立大气-海洋耦合模式。其对模拟精度的提高是十分必要的
台风是台风浪生成的主要动力因素，因此在波浪的模拟中考虑风场的影响是必不可少的，波浪对于大气的影响是不可忽略的，分为动力作用和热力作用。在动力作用中，大气传递动量到上层海洋，驱动表层海水运动，部分动能被海浪场吸收，因此动力作用会减弱台风强度；在热力作用中，海浪会增强海表感热、潜热通量对于大气的传递，从而增强台风强度。因此为了提高风场和波浪场的模拟精度，需要建立大气-海浪的实时双向耦合模式。其可以较好地改善台风强度的模拟效果，但对台风路径的改善程度较小。
台风过程中海洋内部也有强烈的相互作用，因此考虑海洋-海浪耦合模式，实现其计算也是十分重要的。
由上文可知，大气－海洋耦合可以改善台风过程的风场、流程、温度场的模拟效果，大气－海浪耦合模式可以可以较好地改善台风强度的模拟效果，海浪－海洋耦合模式较好地改善了流场和波浪场的模拟结果。因此，更优化的耦合方式正在由两者互相耦合的计算模式向三者两两耦合的计算模式发展，大气－海洋－海浪耦合模式就在此基础上建立起来了。国内外目前建立的海气浪耦合模式主要基于结构化网格，这对于实际岸线的刻画是不利的，因此引入非结构网格的数值模式，例如 FVCOM 海洋模型，可以模拟复杂岸线对流场和温度场的影响，改善模拟结果。
卫星资料同化研究
卫星资料同行是在资料通话的基础上发展起来的，资料同行的理论基础来源于气象学中的分析技术。资料同化的含义是，基于统计“最优”的目的，将多种不同形式的观测数据融合到数值模拟模式中，从而建立起实测值与数值模拟值之间的相互协调关系，在观测资料足够多的前提下，数值模拟模式通过不断导入、整合、调整观测数据，从而使模拟结果越来越接近实际情况，最终得到的模拟结果达到在统计意义上最合理、最准确的效果。
资料同化理论的发展较早，上个世纪 60 年代开始，同化的基本概念形成，此时的同化方法以逐步订正法为主。到上个世纪 80 年代，最优插值法成为当时主导的同化方法，在这一时间段内变分法被提出并逐渐形成。90 年代，变分方法渐渐成熟并开始得到应用。随着卫星的出现，卫星遥感资料的高质量、全球性、高频次、高精度等优点使用同化效果得到了极大的提高，目前各国气象部门普遍采用卫星遥感资料的直接同化。21 世纪初，提出了混合资料同化方法，例如三维变分同化法。
目前世界上采用三维变分同化进行大气模拟的系统有 GSI 同化系统和 WRF 大气模式。GSI（Grid Statistical Interpolation）业务同化系统是美国环境预报中心（NCEP）所采用的同化系统，主要用于全球预报、区域预报以及飓风预报，是目前世界上较先进和成熟的同化系统之一。WRFDA（WRF Data Assimilation）同化模块是 WRF 大气模式中一个不依赖主模块的，可以单独安装编译单独使用的模块。
当然，卫星资料同化也不是完美无瑕的，由于卫星数据也是观测资料，必然存在仪器的观测误差，同时还有辐射传输模式造成的系统性偏差、统计学的偶然误差等，因此卫星资料同化还需要一定的“修正”方法。总结台风过程模拟的工作可以发现，目前利用大气－海洋－海浪耦合模型和卫星数据同化进行台风过程模拟的工作还不多见。
水文频率分析方法研究
正确获取波高的多年分布规律，从而合理地确定不同重现期的设计波高数值，是十分关键的。最传统的方法是采用全部实测波浪数据，利用不同的坐标转换，按直线外延推求不同重现期的设计波高。这种方法的本质是依据经验对直线外延，有两个主要缺点，其一：采用不同的定线方法，对计算结果的影响较大，任意性和随机性较大；其二：对于未完全开发的区域，往往没有长期的波浪实测资料，所以样本数据的容量不够。
随后发展出了年最大值分析法，即对年最大波高组成的系列， 选配一条合适的理论频率曲线，外延推求多年一遇设计波高。其中应用于水文频率统计的概率分布函数主要有皮尔逊 III 型分布、对数正态分布、耿贝尔第一型极值分布和威布尔分布等。这种方法引进了多种概率分布函数，提供了多种科学的定线方法，解决了以往定线随机性的问题。但是无法解决样本数据容量过小的问题，因为波浪资料的年限往往不够长，由几十个或十余个经验点数据选配一条理论频率曲线，任意性还是比较大的。
泊松-耿贝尔复合极值分布： 首先根据台风统计资料，经过分析得出影响某一个海域的台风发生频次极好地符合泊松（Poisson）分布；然后检验每次台风影响下形成的波高，得到波高分布在包伟尔几率格纸上呈现直线关系，说明台风波浪波高原始分布符合耿贝尔（Gumbel）分布，由此得到了一种海洋工程中推算设计波高的方法。《港口与航道水文规范》（JTS145-2015）中规定，对于台风多发海域，某一波向一年中出现一个以上较大台风波高时，可按台风波高的最大值系列取样，采用泊松一耿贝尔复合极值分布确定不同重现期的设计波高。
随着海洋、海岸工程的发展，采用联合分布方法计算风、浪、流联合频率越来越受到人们的重视。因为台风过程各要素的计算结果中，最大风速、最大流速、最大波高往往不在同一时刻出现，并且各要素最大值的组合形式是复杂多样的，若采用传统的单一要素频率分析法，其结果往往偏于过于保守。联合分布方法以对海洋工程影响最大的要素作为主导要素，考虑了与该要素最大值同时发生的其他要素的较大值，更符合实际情况，在保证设计安全的情况下有可能降低工程造价。
本文的主要研究工作
目前的大多数研究所采用的模拟方法是数值模型模拟出风场，再利用风场驱动海洋模型和海浪模型获得流场、温度场和波浪场，这样的模拟方法局限于单一模型的独立模拟，且模拟精度与实际情况偏差较大，受制于风场的模拟精度。因此，本文的模型从两方面改善台风过程中各数值场的模拟精度。
其一是改善风场模拟本身的精度，因为受风场初始场资料的分辨率较低和数值模型积分过程的计算误差影响，模拟得到的风场结果会有台风移动路径不准确、台风强度偏弱等问题，由此产生了利用卫星资料对模拟结果进行校正的方法–卫星资料连续同化。卫星资料具有时空分辨率较高、覆盖面积较广的特点，在很大程度上弥补了海洋气象站的常规观测资料稀少的缺点。
其二是通过模型耦合提高模拟精度。由于台风过程不是单一的大气作用过程，而是一个复杂的大气-海洋-海浪相互作用的过程，因此模拟思路应该更向实际情况发展，不局限于单一模型的独立模拟，也不再局限于离线耦合，而是向多个软件的实时耦合发展，建立大气-海洋-海浪的实时耦合模型，这样的模拟思路在原理上更科学更符合实际，且对于台风风场、海表流场、温度场和波浪场的模拟效果都有相应改善。
另外，对于各设计要素的确定，传统方法大多是对各设计要素分别进行概率分析，然后选取其某一重现期值作为设计标准。但是各种极端情况同时出现的概率极小，如最大风速、最大波高同时发生在同一时刻的概率极小，所以传统方法是不符合实际、也是偏于保守的，会导致工程成本估算过高，因此为合理反映海洋工程在实际中受风、浪的影响，获得风、浪的联合分布更具有实际价值。
为了提高台风过程风、浪、流模拟精度，本文将采用 MCT 耦合器对中尺度大气模型 WRF、非结构化网络海洋模型 FVCOM及非结构化网格波浪模型 SWAN 进行耦合，并在计算过程中利用 WRF 大气模式的资料同化模块 WRFDA（WRF Data Assimilation）对风场进行卫星资料同化，即建立大气-海洋-海浪实时耦合模型与卫星数据同化的联合运用模型，对 1999-2018 年影响海南岛海域的台风过程风场、海表流场、波浪场进行数值模拟，最后利用水文频率统计法获得工程所需的设计要素。
基于卫星同化的大气-海洋-海浪实时耦合模式
数值模型简介
由于台风过程不仅涉及大气本身的变化，而且涉及海洋、波浪的变化，因此分别采用大气、海洋和波浪模型描述这些变化过程并通过模型耦合描述他们之间的相互影响。
耦合器及耦合方案
耦合器
大气－海洋－波浪耦合模式基于 MCT（Model Coupling Toolkit）耦合器建立。MCT 耦合器是一款用来建立耦合模式的开源程序工具包。MCT 支持并行耦合系统的各子模式间多个分布式变量的数据交换。MCT 采用 FORTRAN90 编写，包含一系列 FORTRAN 模块，各子模式调用这些模块实现数据的发送和接收。MCT 开源代码
耦合方案
耦合模式由主程序调用 WRF、FVCOM 和 SWAN 子模式同时独立计算，在设定的某一计算时间，各子模式调用MCT子程序进行数据的发送和接收，实现子模式两两之间的实时数据交换。由于 WRF 采用结构化网格，FVCOM 和 SWAN 采用相同的非结构化三角形网格，WRF 和 FVCOM、SWAN 之间进行变量交换时需要进行插值，而 FVCOM 和 SWAN 之间可以直接传递变量。模式耦合机制如图 1 所示。
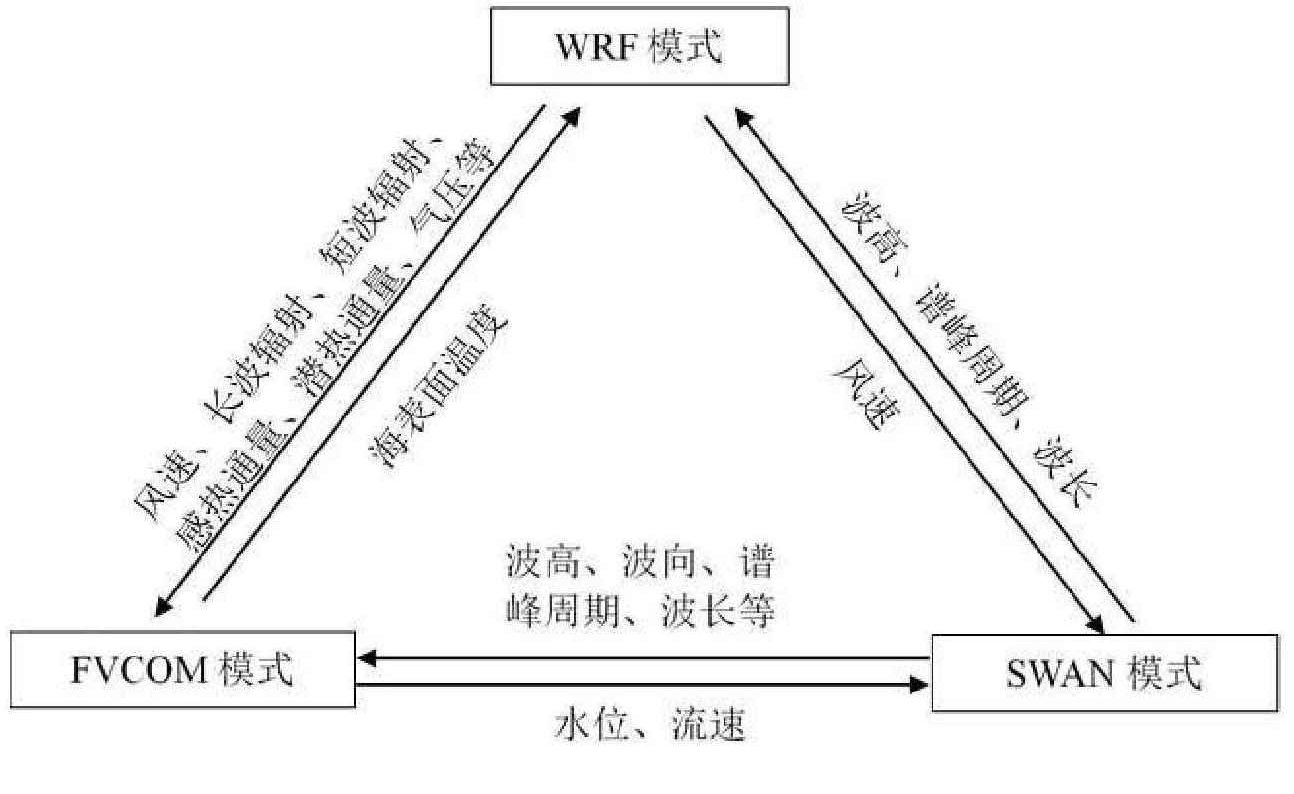图 1. 模式耦合机制
大气-海洋耦合机制
大气对海洋的作用
大气与海洋耦合中，台风过程中的海气相互作用主要体现在海面大风造成上层海洋强烈的搅拌和混合，改变其热力结构。大气对海洋产生强迫作用，主要包括海表面风应力、长波辐射、短波辐射、感热通量、潜热通量、海面以上 10m 处风速。FVCOM 模式在笛卡尔坐标下的三维动量方程和连续性方程为：
$$
\left\{\begin{matrix}
\frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} + w \frac{\partial u}{\partial z} - fv = -\frac{1}{\rho_0} \frac{\partial (P_H + P_a)}{\partial x} - \frac{1}{\rho_0}\frac{\partial q}{\partial x} + \frac{\partial }{\partial z}(K_m \frac{\partial u}{\partial z} ) + F_u \\
\frac{\partial v}{\partial t} + u \frac{\partial v}{\partial x} + v \frac{\partial v}{\partial y} + w \frac{\partial v}{\partial z} + fu = -\frac{1}{\rho_0} \frac{\partial (P_H + P_a)}{\partial y} - \frac{1}{\rho_0}\frac{\partial q}{\partial y} + \frac{\partial }{\partial z}(K_m \frac{\partial v}{\partial z} ) + F_v \\
\frac{\partial w}{\partial t} + u \frac{\partial w}{\partial x} + v \frac{\partial w}{\partial y} + w \frac{\partial w}{\partial z} = -\frac{1}{\rho_0} \frac{\partial q}{\partial z} + \frac{\partial }{\partial z}(K_m \frac{\partial w}{\partial z} ) + F_w \\
\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} = 0
\end{matrix}\right.
\tag{1}
$$
温度扩散方程为：
$$
\frac{\partial T}{\partial t} + u \frac{\partial T}{\partial x} + v \frac{\partial T}{\partial y} + w \frac{\partial T}{\partial z} = \frac{\partial }{\partial t}(K_h \frac{\partial T}{\partial z} ) + F_T
\tag{2}
$$
式中，$x,\ y$ 和 $z$ 分别为笛卡尔坐标系中坐标，分别代表水平和垂直方向；$u,\ v$ 和 $w$ 分别是流速沿 $x,\ y,\ z$ 方向的分量；$T$ 代表温度；$f$ 是科氏力参数；$\rho_0$ 为海水密度；$P$ 为压力；$K_h$ 代表紊动动能的垂向扩散系数。$F_u$ 代表 $x$ 方向的水平动量，$F_v$ 代表 $y$ 方向水平动量，$F_t$ 代表温度扩散项。
流速 $u$ 和 $v$ 表面边界条件为：
$$
K_m(\frac{\partial u}{\partial z}, \frac{\partial v}{\partial z}) = \frac{1}{\rho_0}(\tau_{sx}, \tau_{sy})
\tag{3}
$$
$$
(\tau_{sx}, \tau_{sy}) = C_d \sqrt{U_{10}^2 + V_{10}^2}(U_{10},\ V_{10})
\tag{4}
$$
其中，$(\tau_{sx}, \tau_{sy})$ 是表面风应力的 $x、y$ 方向分量，$C_d$ 为拖曳力系数，$(U_{10}，V_{10})$ 为海面上空 10m 处风速。
而温度的表面和底部边界条件为：
$$
\frac{\partial T}{\partial z} = \frac{1}{\rho c_p K_p} [Q_n(x,y,t) - SW(x,y,\zeta,t)]
\tag{5}
$$
$$
\frac{\partial T}{\partial z} = -\frac{A_H tan \alpha}{K_h} \frac{\partial T}{\partial n}
\tag{6}
$$
其中 $Q_n(x,y,t)$ 是表面净热通量，包括四部分：向下的短波辐射通量和长波辐射通量，感热通量和潜热通量；$SW(x,y,\zeta,t)$ 是到达海表面的短波辐射通量，$C_p$ 是海水的比热容，$S_H$ 是水平热扩散系数，$\alpha$ 是底部地形的坡陡，$n$ 是水平坐标。
耦合时，大气模式传递到海洋模式中的海面上空 10m 风速用以计算表面风应力，影响流场的求解。而传递的长波辐射、短波辐射、感热通量、潜热通量用以计算 $Q_n(x,y,t)$ 和 $SW(x,y,\zeta,t)$，影响温度扩散方程的求解，改变海表温度分布。
海洋对大气的作用
海洋向上的热量通量是台风系统发展和维持的重要热源，其主要通过海表温度来体现，海表温度既影响台风的形成和移动，又影响台风强度。耦合模式中，海洋模式模拟的海表温度 SST 传递至 WRF 模式中，通过表面层方案更新大气模式下垫面温度，继而通过下垫面温度影响边界层方案、积云对流方案和辐射方案计算，对表面通量（长波辐射、短波辐射、表面应力等）和大气状态（位温、湿度、云雨等）产生影响，影响模拟的台风强度和路径。由于涉及方程表达式较多，本文不再赘述。
大气-海浪耦合机制
海浪对大气的作用
气浪耦合中，大风条件下，强浪场显著改变了海表状态，直接影响海气界面上的动量、热量和物质交换过程，这种影响通过海表粗糙度的变化来实现。在 WRF 模式中需要计算表面动量 、热量 和湿度 ，三者分别表示如下：
$$
F_m = \rho_1 C_m |\vec{V_{SL}}|^2
\tag{7}
$$
$$
F_h = \rho_1 c_p C_{hq}(\theta_{sk} - \theta_1)
\tag{8}
$$
$$
F_q = \rho_1 LC_{hq}M(q_{vsk} - q_{v1})
\tag{9}
$$
其中，$C_m$ 为动量交换系数，$C_{hq}$ 为热通量和水汽通量有效交换系数，具体关系式为：
$$
C_m = \frac{U^2_* }{|\overline{V_{SL}}|^2}
\tag{10}
$$
$$
\vec{V_{SL}}^2 = u^2 + v^2
\tag{11}
$$
$$
C_{hq} = u_*k[\psi_h(\frac{Z_r}{L_{MO}}) - \psi_h(\frac{Z_{OT}}{L_{MO}}) + ln(\frac{Z_r}{Z_{OT}})]^{-1}
\tag{12}
$$
其中，$Z_r$ 是观测高度，$Z_{OT}$ 是有温度贡献的海表面粗糙长度，$L_{MO}$ 是 Monin-Obukhov 长度。
$$
L_{MO} = \frac{-u_*^3 \bar{\theta}}{kg(\theta_{sk} - \theta_{1})}
\tag{13}
$$
摩阻速度 $u_$ 和由动量贡献的海表面粗糙长度 $Z_{om}$ 有关，$u_$ 和 $Z_{om}$ 关系式如下：
$$
u_* = k |\vec{V_{SL}}| [\psi_m(\frac{Z_r}{L_{MO}}) - \psi_m(\frac{Z_{om}}{L_{MO}}) + ln(\frac{Z_r}{Z_{om}})]^{-1}
\tag{14}
$$
海面上的波浪将改变海表面粗糙度 $Z_o$ 中的 $Z_{om}$ 大小，通过建立 $Z_{om}$ 和波浪参数之间的关系可以反映波浪对风场的影响：
$$
Z_{om} = f(H_{wave},\ L_{pwave},\ T_{psurf})
\tag{15}
$$
Taylor 等根据实验数据提出了粗糙度关于波高和波陡的关系式：
$$
Z_{om} = 1200.0H_{wave}(H_{wave} / L_{pwave})^{4.5}
\tag{16}
$$
其中，$H_{wave}$ 是有效波高，$L_{pwave}$ 是谱峰周期对应的波长。
WRF 模式的 MYNN 近地面层方案中可以选用 Taylor 参数化方案，但波浪要素通过考虑风速的经验公式计算。本文对 Taylor 参数化方案计算方法进行改进，耦合时，WRF 模式海表粗糙度根据 SWAN 模式有效波高、谱峰周期和谱峰波长等结果实时更新，而不是采用经验公式计算波浪要素。
大气对海浪的作用
热带气旋过程中，强风的作用引起海表形成较大的风浪，耦合中，大气模式向海浪模式传递海面上 10 米处的风速作为波浪场的驱动风场。
SWAN 模式的建立基于包含源汇项的波作用谱平衡方程，描述风浪生成及其在近岸区的演化过程。在直角（笛卡尔）坐标系下，波作用谱平衡方程的表达式为：
$$
\frac{\partial}{\partial t} N + \frac{\partial}{\partial x} C_x N + \frac{\partial}{\partial y} C_y N + \frac{\partial}{\partial \sigma} C_\sigma N + \frac{\partial}{\partial \theta} C_\theta N = \frac{S}{\sigma}
\tag{17}
$$
其中，$N$ 为波作用密度谱，$S$ 为用谱密度表示的源汇项；$\theta$ 为波向，即各谱分量垂直于波峰线的方向；$\sigma$ 为波浪的相对频率，即在随水运动的坐标系中观测到的频率；$C_x、C_y$ 为 $x、y$ 方向的波浪传播速度；$C_\theta、C_\sigma$ 为 $\theta、\sigma$ 空间的波浪传播速度。
SWAN 模式中波作用谱平衡方程的源汇项表达式为：
$$
S = S_{in} + S_{ds,w} + S_{da,b} + S_{da,br} + S_{nl4} + S_{nl3}
\tag{18}
$$
其中，$S_{in}$ 表示风能输入，$S_{ds,w}$ 表示由白浪引起的波能耗散，$S_{ds,b}$ 表示由底部摩擦引起的波能耗散，$S_{ds,br}$ 表示水深变浅引起的波浪破碎，$S_{nl4}$ 表示四波非线性相互作用，$S_{nl3}$ 表示三波非线性相互作用。
风能输入 $S_{in}$ 由两部分组成：线性增长项和指数增长项。风能输入表达式为：
$$
S_{in} = A + BE(\sigma,\theta)
\tag{19}
$$
式中，$A$ 表示线性增长项，$BE$ 表示指数增长项。在 SWAN 模式中，输入项是海面上空 10m 处的风速 $U_{10}$，而 $A$ 和 $BE$ 的计算过程中采用摩擦速度 $U_*$，两者之间的关系式为：
$$
U_* = C_D U_{10}^2
\tag{20}
$$
其中，$C_D$ 表示风拖曳力系数：
$$
C_D = (0.55 + 2.97 \widetilde{U} - 1.49 \widetilde{U}^2) \times 10^{-3} \\
\widetilde{U} = U_{10} / U_{ref}
\tag{21}
$$
其中，$U_{ref}$ 是参考风速。
因此，大气模式模拟的海面以上 10m 风速影响波浪模式中的风能输入项，进而影响波作用谱平衡方程的求解。
海洋-海浪耦合机制
海浪对海洋的作用
波浪会对水流的运动过程、分布形式产生复杂影响，主要表现为：波浪辐射应力产生驱动力、海面粗糙度增大引起表面风应力的增加以及底部剪切应力改变导致底部摩阻的增加，本文仅考虑波浪辐射应力的影响。在笛卡尔坐标系下，考虑三维辐射应力的 FVCOM控制方程，请移步原文。
耦合中，海浪模式传递波高、波向、波长等给海洋模式FVCOM，FVCOM 基于传递的波参数计算波速、波数、波能与波浪辐射应力，进而求解控制方程。
海洋对海浪的作用
水流也会对波浪的演变过程和形态产生复杂影响，水流流向和波浪传播方向异同会引起波要素（例如：波速、波长、波陡等）的变化。SWAN 模式波作用谱平衡方程，请移步原文。
模型耦合时，海洋模式传递流速和水位给海浪模式，水深和背景流场的变化影响波浪模式中的频率迁移和波浪折射，影响波作用谱平衡方程的求解。
卫星资料连续同行
WRFDA 概述
WRF 大气模式的资料同化模块 WRFDA（WRF Data Assimilation）是一个不依赖主模块的，可以进行单独编译并且单独使用的模块。本文采用同化模块版本为 WRFDA 3.8.1（目前最新为：WRFDA 4.5.1），可以实现的功能包含：混合资料同化（Hybrid）、集合卡尔曼变换（ETKF）、三维变分同化（3D-Var）、思维变分同化（4D-Var）。WRFDA 系统包括观测数据前处理（OBSPROC），主区域同化及侧边界条件更新，背景场误差协方差构造（GEN BE）等功能模块，各模块以及它们与 WRF 系统的其余部分的关系如图 2 所示。
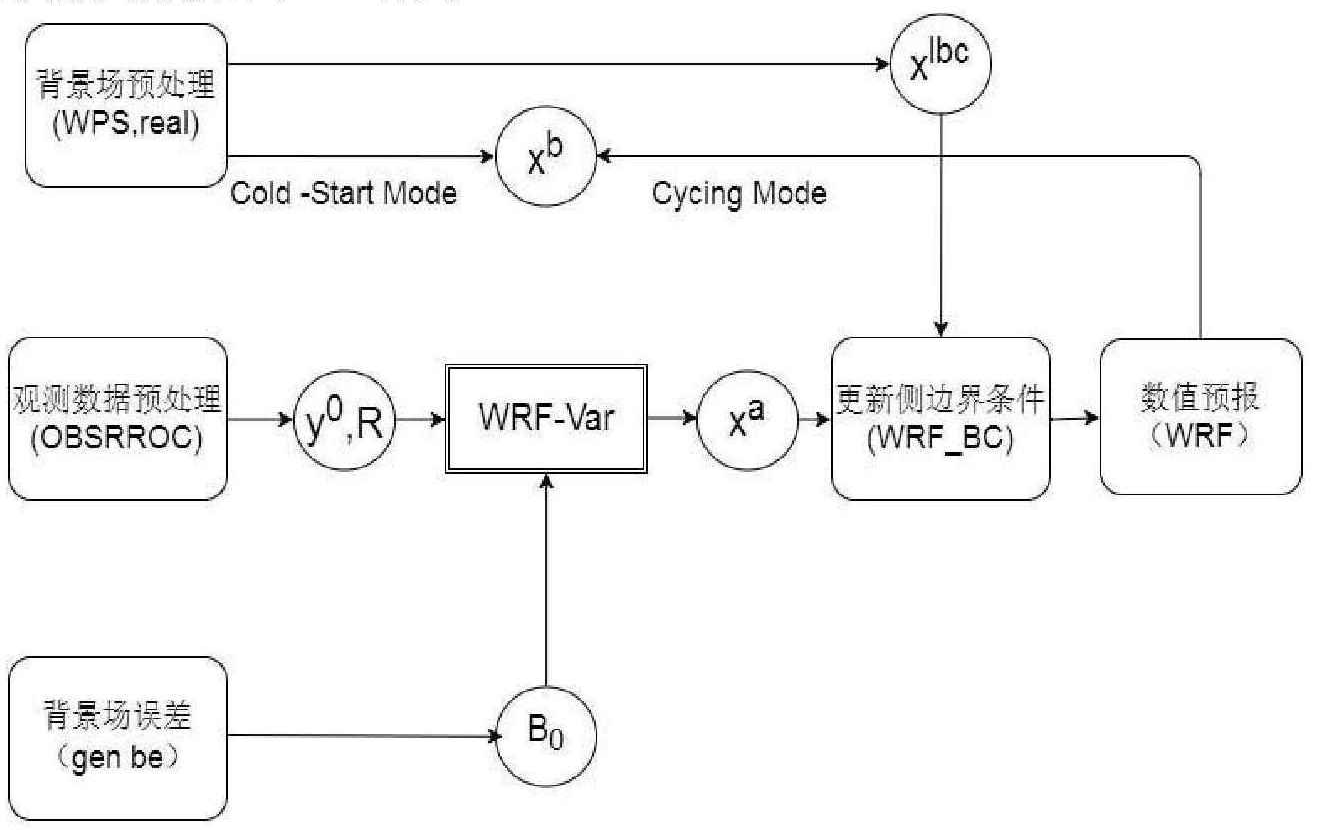图 2. WRFDA运行流程图
三维变分同化原理
WRFDA 中的三维变分同化系统是基于 MM5 大气模式的三维变分同化系统（3D-Var）发展起来。变分数据同化系统的基本原理是通过迭代算法求解指定的目标函数以获取对于真实气候状态的一个最优估计。变分同化的内容主要包括目标函数得确定，观测算子及预报模式的选取，背景场误差协方差 $B$ 的计算，控制变量 $v$ 与分析整理 $\delta_x$ 的变换关系 $U$ 的建立、下降算法选取与目标函数计算。具体步骤请移步原文。
卫星资料的连续同化通过 WRF 大气模式的资料同化模块 WRFDA（WRF Data Assimilation）来实现，本文的同化方案采用三维变分同化。图 3 所示为一个模拟时间步长的耦合-同化过程：在初始耦合计算完成后生成了 WRF 风场的初始场和边界条件，然后再单独运行 WRFDA 模块进行卫星资料同化，并更新 WRF 的初始场和边界条件，再以新的初始场和边界条件进行耦合模型计算，得到同化后的 WRF 的风场数据、FVCOM 的流场数据和 SWAN 的波浪场数据，至此完成了第一个模拟时间步长的耦合一同化计算，之后的计算以此类推，最终完成所有时间步长的耦合一同化计算，实现连续耦合一同化计算。
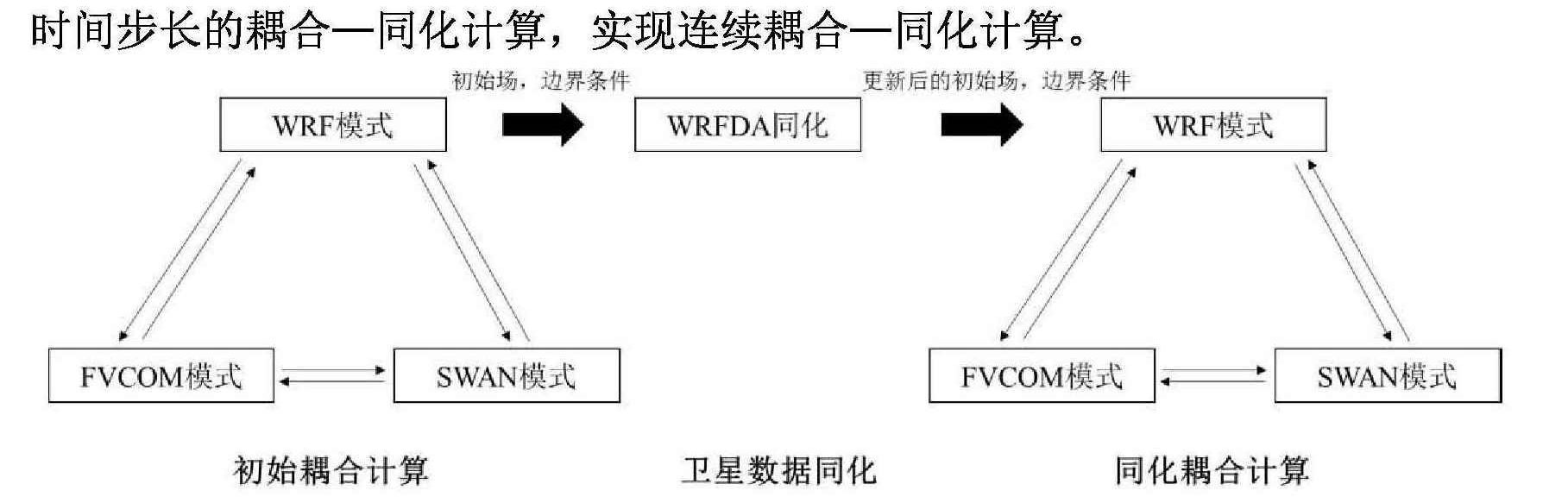图 3. 耦合-同化过程
本章小节
本章从模式概述以及控制方程两方面对本课题所采用的中尺度大气模式 WRF、非结构化网格海洋模型 FVCOM、第三代海浪模式 SWAN、大气-海洋-海浪耦合机制、卫星资料同化原理以及耦合模拟-数据同化联合模型进行了介绍。
台风算例与耦合同化计算方案的确定
风场资料的选取
本文主要针对海南岛附近海域进行分析。根据热带气旋的强度划分依据，并结合台风实时发布系统 和 中国台风网，对1999 - 2018 年间经过太平样的共计 528 场热带气旋进行了路径观察和强度分析。具体资料选取，请移步原文。
计算区域与网格划分的确定
影响 WRF 模型计算的物理参数有很多，其中计算区域范围和网格精度是两个十分关键的影响因素。具体计算区域与网格划分的确定请移步原文。
为了取得更准确的风场模拟结果，且在一定程度上保证计算资源与模拟结果的平衡，本文的 WRF 大气模式采用水平方向的大小网格嵌套计算，地形范围在合理程度上进行扩大，覆盖至菲律宾海域，地形范围如图 4 所示，主区域 D1（大模型）与嵌套区域 D2（小模型）均采用正方形网格。主区域 D1 的经度范围为 $104.07^\circ E$ ~ $130.28^\circ E$，纬度范围为 $0.15^\circ N$ ~ $40.63^\circ N$，其空间分辨率为 12km，网格数为 $372 \times 199$；嵌套区域 D2 的经度范围为 $106.51^\circ E$ ~ $116.38^\circ E$，纬度范围为 $16.23^\circ N$ ~ $22.26^\circ N$，其空间分辨率为 4km，网格数为 $168 \times 258$。垂向分层层数采用不均匀的 35 层。
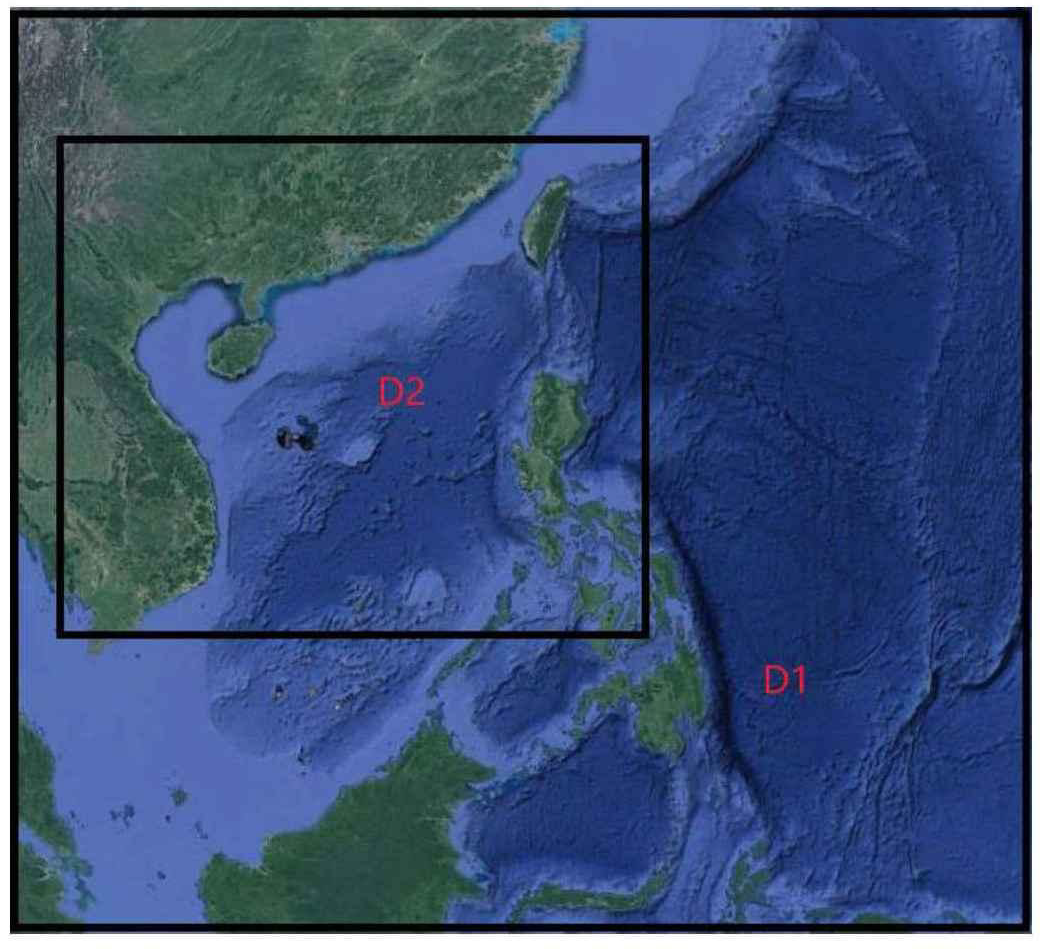图 4. 计算范围地形
海洋模型 FVCOM 和海浪模型 SWAN 的水平网格为非结构化三角形网格，采用经纬坐标，近岸和水深变化剧烈处采用局部网格加密最小网格点间距约 500m，开边界处网格较疏，最大网格点间距约 20km。地形纬度范围为 $11.60^\circ N$ ~ $25.38^\circ N$，经度范围为 $105.61^\circ E$ ~ $119.65^\circ E$。模型单元数 50785，网格节点数为 26418，地形范围和网格示意图如图 5。FVCOM 海洋模型垂向采用 $\sigma$ 坐标分为 15 层。
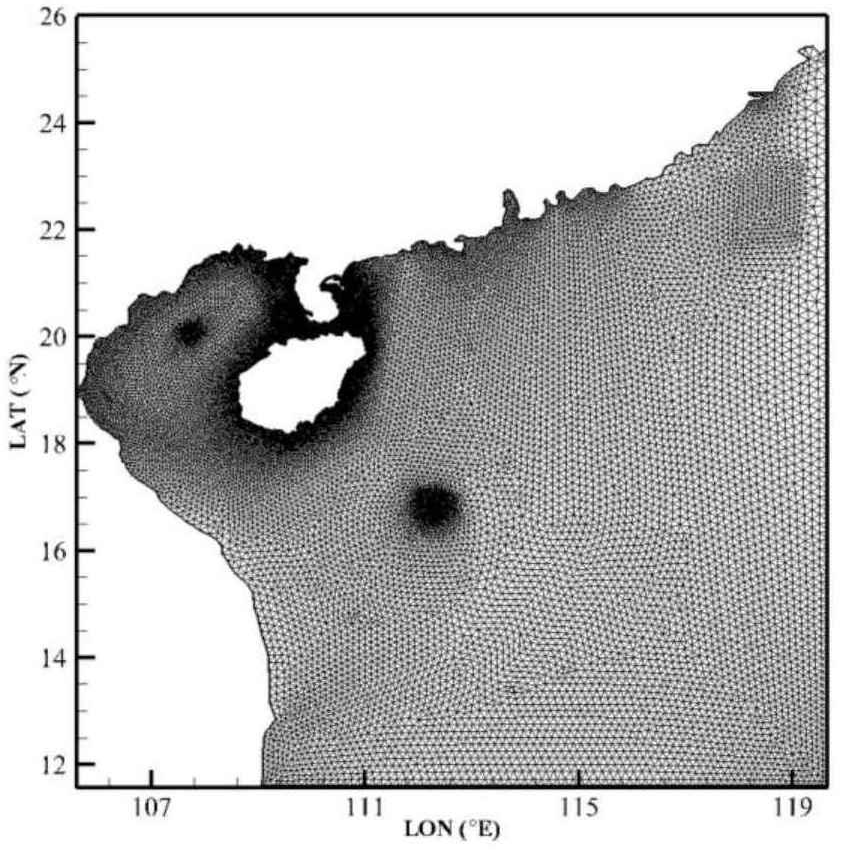图 5. FVCOM 模式和 SWAN 模式的计算范围和网格
耦合模式计算方程的确定
WRF 模式计算方案的确定
WRF 大气模式是通过选取不同的计算参数来模拟相应的气象过程，不同的计算参数对于台风模拟的路径、强度影响较大，因此针对模拟研究区域选取合适的计算参数是十分关键的。
本文采用的是 W-F-S-A 耦合同化模式，其中耦合模式相对于单一的 WRF 模式有所改进。单一的 WRF 模型中一般需要引入参数以描述海浪的作用。近年来，国内外普遍采用海表面粗糙度对海浪的影响进行参数化因此耦合模式基于 Taylor 和 Yelland 公式对原始 WRF 计算模型进行了修改，建立了海表面粗糙度 $Z_{om}$ 与波浪参数（波高、谱峰周期、波长）的关系，将其加入至 MYNN 选项中：
$$
Z_{om} = 1200.0 H_{wave}(H_{wave} / L_{wave})^(4.5)
\tag{22}
$$
并同时改进 WRF 计算模型中的海表面层和海表边界层的物理模式。本文选取的 WRF 模型参数如表 1 所示。
表 1. WRF 模式参数选择结果
| 项目 | 方案 |
|---|---|
| 陆面过程 | Noah-MP |
| 积云参数化 | Kain-Fritsch |
| 微物理过程 | WSM6 方案 |
| 短波辐射 | Dudhia 方案 |
| 长波辐射 | RRTM 方案 |
| 表面层 | Monin-Obukhov-Janjic(Eta) 方案；MYNN 方案 |
| 边界层 | Mellor-Yamada-Janjic(Eta) 方案；MYNN 2.5 阶方案 |
耦合模式计算方案的确定
WRF 主区域积分时间步长根据手册的推荐，取为计算网格精度 12km 的 6 倍，即 72s，主区域 D1 与嵌套区域 D2 采用双向计算。为排除非耦合和耦合试验初始海表温度不同导致的海气界面差异，温度初始场的海表温度均采用 NECP 的全球日平均数据 RTG_SST，潮位开边界使用 MIKE21 提取，并提前计算 ７ 天获得耦合模拟时的初始流场。FVCOM 模型积分时间步长取 5s。SWAN 模型由较大范围的波浪模拟结果提供边界场和初始场，计算时间步长 300s。WRF、FVCOM 和 SWAN 三者耦合交换时间步长取 600s。
同化方案的确定
卫星资料的选取
要通过卫星资料连续同行改善风场模拟精度，前提是选择合适的卫星遥感资料。本文选取 NOAA-15、NOAA-18 两颗卫星的 AMSU-A 亮温资料进行同行。其中 AMSU-A 探测器包含 15 个通道，第 4-14 号通道为 AMSU-A1，主要探测大气温度数据，第 1、2、3 和 15 号通道为 AMSU-A2（窗区/表面），主要探测降水量和地表信息。本文采用的传感器通道为第 5~9 号通道。
计算模式的确定
大气辐射传输模式类型的选取对于同化模块是十分关键的，WRF 中采用了国际上应用较为广泛的两种快速辐射传输模式：CRTM 与 RTTOV。经过前人的实验对比，本文选择 CRTM 快速辐射传输模式 2.1.3 版本（目前为 V 2.4.0）作为同化时的大气辐射传输模式。
同化方法的确定
本文采用 GSI-3Dvar 三维变分同化，无法实时融合各时段的卫星资料数据，只能选取指定同化窗口内的卫星资料数据作为同化数据进行融合分析，且单次童虎窗口的时间步长不宜过大，不可能覆盖整个台风模拟时间段。所以，本文采取卫星资料连续同化的方法改善这一缺陷，以 6h 间隔资料循环同化方案为例进行说明，若某一卫星经过研究区域的时间间隔约为 12h，采取循环同化的优点在于，若前一次 6h 的同化窗口内没有识别到卫星数据，可以在下一个 6h 的同化窗口中进行识别，从而在一定程度上保证模拟同化时间段内只有很少的卫星资料没有识别，提高卫星资料的利用率和卫星数据的同化效果。综上所述，本文采用 GSI-Dvar 三维变分同化，同化方法采用 6h 间隔资料循环同化。
本章小节
本章对 1999-2018 年台风样本数据的选取理由及结果进行了介绍，并说明了风场初始再分析资料获取的来源。此外，还对算例模拟方案三大部分的设置过程进行了详细说明，一是模型计算区域、网格划分非确定理由和结果；二是耦合模式中各模型计算方案的确定理由和结果；三是同化方案的确定理由和结果。
台风过程的风场模拟
台风风场特征
上层海洋对台风的响应主要受制于风应力，风场强迫使上层海洋产生波浪与海流，改变海水温度分布，台风风场是影响台风过程上层海洋状态的主要因素。关于耦合同化模拟得到的风场过程，请移步原文。
台风路径和风场强度
对台风风场数值模拟的结果除了风场特征分析外，还需要通过与实测资料的对比验证分析模拟误差，本文的实测验证数据采用 CMA-STI 西北太平洋热带气旋最佳路径数据集，该数据集是研究影响我国海域台风常用的数据校对资料。其数据基础建立在全国各级气象站每年在热带气旋过后所收集到的常规和非常规气象观测资料上，由中央气象局委托，上海台风研究所主导，对每年的热带气旋的强度和路径资料进行分析、汇总、编制，形成台风年鉴数据集。CMA-STI 数据集提供自1949年开始的，发生在西北太平洋海域的热态气旋数据，数据内容包括台风强度等级、台风中心经纬度坐标、台风中心最低气压、台风中心最大风速等信息。具体由 W-F-S-A 耦合同化模式模拟得到的南海海域10场台风的路径、最大风速结果与相应时刻的 CMA-STI 数据集的对比分析图，请移步原文。
对于台风路径模拟，大部分台风的平均模拟误差均在 35km 一下，从单台风的路径模拟结果来看，模拟误差最大的为 201329 号台风“罗莎”，模拟平均误差为 42km，通过改变地形、物理参数重新模拟并未得到明显改善，可能是初始的 FNL 再分析资料本身存在的系统误差导致。路径模拟误差最小的为 201409 号台风“威马逊”，模拟平均误差为 18.9km。值得注意的是，对于路径变化比较“曲折”的台风，即路径中有较多幅度大的拐点，甚至存在“蝴蝶结”型的路径，对于这些台风，W-F-S-A 耦合同化模式也能较好地刻画出台风移动的路径。
对于台风中心附近最大风速模拟结果与 CMA-STI 数据对比，可以看出，模拟结果与数据集在台风风速变化趋势方面保持一致，大部分台风强度均为先增强后减弱的变化过程。从台风强度对比图中还可以看出，模拟初始时刻的台风风速结果往往较弱，低于 CMA-STI 数据集结果，其原因主要是 WRF 计算模式对于初始场的模拟结果不够理想，通过耦合-同化已经得到了相应的改善，但与实际情况相比仍存在 15m/s 左右的误差，但是本文已经采取扩大模拟时间的方式，在最大范围内保证模拟初始时刻不发生在研究区域附近，排除初始场误差。排除初始阶段的模拟结果，大部分台风的风速模拟误差均在 8m/s 以下，从当场台风的强度模拟结果来看，模拟误差最大的为 200521 号台风“启德”，平均误差为 10.2m/s；模拟误差最小的为 201409 号台风“威马逊”，平均误差为 1.5m/s，基本与 CMA-STI 数据集一致。
综上所述，由 W-F-S-A 耦合同化模式模拟得到的 70 场台风的路径、强度结果与 CMA-STI 数据集的误差在合理范围内，模拟结果可作为后续推算设计要素的数据依据。
耦合-同化效果分析
关于作者所采用的 W-F-S-A 耦合同化模式与纯 WRF 模式的差异分析，请移步原文。综合分析可得，作者采用的 W-F-S-A 耦合同化模式，无论在台风路径的模拟还是台风风速强度的模拟均优于 WRF 模式。
最大风速计算结果
测点的选择
本文的研究区域为海南岛附近海域，所以选取海南岛岸线 30m 等深线上的八个点作为研究测点，如图 6 所示，测点经纬度数据见表 2。
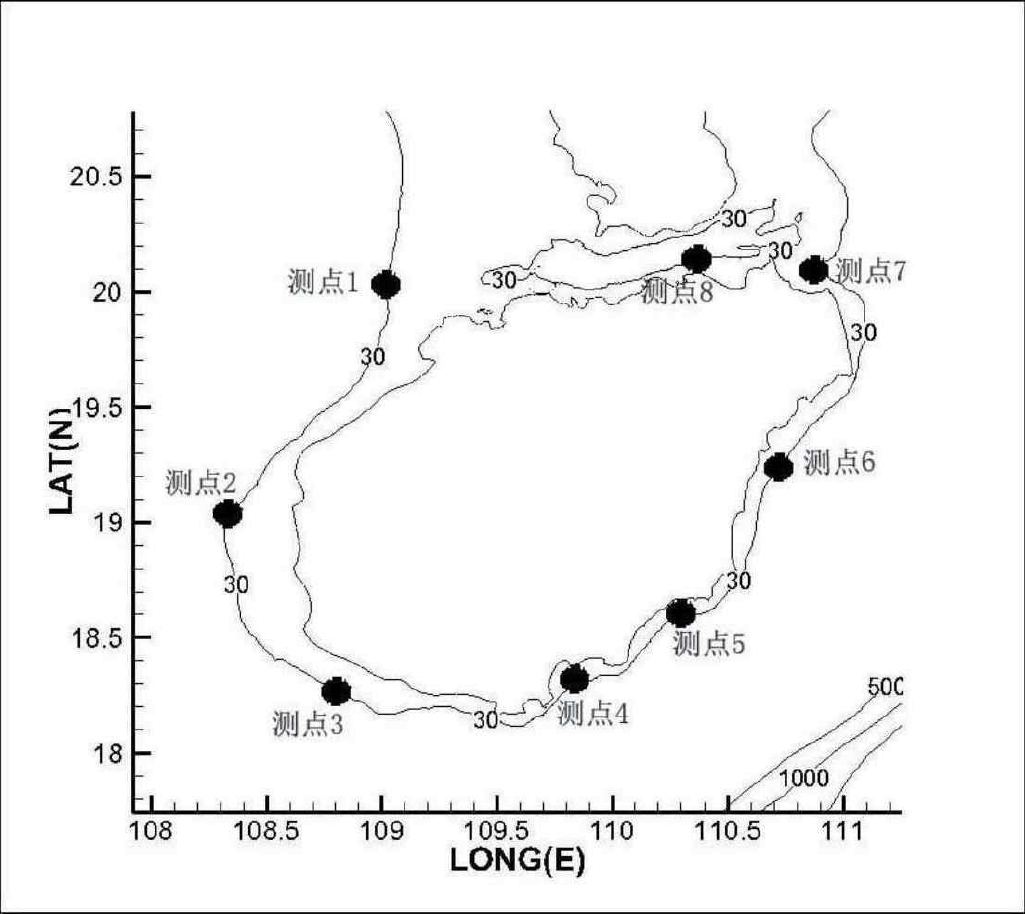图 6. 测点位置图
表 2. 测点经纬度坐标
| 测点编号 | 经度（ $^ \circ E$ ） | 纬度（ $^ \circ N$ ） |
|---|---|---|
| 1 | 109.02 | 20.03 |
| 2 | 108.33 | 19.04 |
| 3 | 108.80 | 18.26 |
| 4 | 109.84 | 18.32 |
| 5 | 110.30 | 18.60 |
| 6 | 110.72 | 19.24 |
| 7 | 110.87 | 20.09 |
| 8 | 110.36 | 20.14 |
研究风向的确定及最大风速的计算结果
对 70 场热带气旋的风向计算结果进行处理。按 N、NE、E、SE、S、SW、W、NW 进行8个方向的划分，统计所有热带气旋计算结果在各测点的风的频率结果。从而确定8个测点的研究风向。统计结果见表 3，研究风向确定结果见表 4，70场热带气旋的最大风速结果请移步原文附录 A。
表 3. 台风期间风向分布统计表
| N | NE | E | SE | S | SW | W | |
|---|---|---|---|---|---|---|---|
| 1号测点 | 11% | 41% | 10% | 10% | 9% | 4% | 6% |
| 2号测点 | 12% | 14% | 8% | 11% | 10% | 5% | 9% |
| 3号测点 | 41% | 11% | 5% | 4% | 9% | 12% | 10% |
| 4号测点 | 13% | 32% | 10% | 7% | 9% | 9% | 9% |
| 5号测点 | 11% | 33% | 12% | 8% | 9% | 8% | 9% |
| 6号测点 | 14% | 34% | 13% | 9% | 8% | 7% | 7% |
| 7号测点 | 13% | 37% | 15% | 9% | 8% | 5% | 5% |
| 8号测点 | 9% | 46% | 10% | 9% | 9% | 5% | 5% |
表 4. 8个测点研究风向的确定
| 测点 | 方向 | 测点 | 方向 |
|---|---|---|---|
| 1号测点 | NE | 5号测点 | NE |
| 2号测点 | NW | 6号测点 | NE |
| 3号测点 | N | 7号测点 | NE |
| 4号测点 | NE | 8号测点 | NE |
本章小节
本章对 1999-2018 年间影响海南岛附近海域的 70 场台风热带气旋，采用 W-F-S-A 耦合同化模式进行模拟。对 2014 年 15 号台风“海鸥”的风场特征进行了分析，模拟结果与前人的研究相符。将模拟得到的台风路径和风场强度与 CMA-STI 西北太平洋热带气旋数据集进行对比验证，验证结果说明模拟得到的 70 场热带气旋风场结果较合理，可以作为后续推算设计要素的数据依据。本章还通过对不同模拟方式模拟结果的比较论证了 W-F-S-A 耦合同化模式的最优性。通过对所有 70 场风速、风向结果的数据处理，确定了 8 个测点的研究风向，统计出 70 场热带气旋的最大风速结果。
台风过程的流场和温度场模拟
台风过程的表面流场特征
在台风旋转风场的作用下，台风路径附近海域会形成旋转流场。台风下的流程具有以下特征：1. 流场具有旋转性，流场中心位于台风移动方向的左后方，流场围绕旋转中心逆时针转动；2. 从流场等值线图中可以看出流场沿台风移动方向呈现明显的带状分布，且大流速区基本位于台风路径的右侧，并且各时刻的最大流速也基本出现在台风移动方向的右后方，因此台风下的流场具有明显的右偏性。
台风过程的海表温度场特征
台风经过海面时，在强风应力的影响下，海洋上下层发生强烈垂直混合，深层冷水上涌到混合层，导致海表温度显著下降。通过模拟实验说明了 W-F-S-A 耦合同化模式相较于 WRF 模式，能较好地反映出台风过境时海表温度下降的现象（具体模拟实验过程请移步原文），与实际情况更相符，说明了采用耦合模式的优越性。
综上所述，台风过程温度场的特征为：1. 低温区场沿台风移动方向呈现明显的带状分布，且低温中心基本位于台风路径的右侧，并且 SST 下降幅度较大的区域也会发生在台风路径右侧的海域，因此台风下的温度场具有明显的右偏性；2. 模拟 66h 时降温范围仍较大，说明温度场的变化较台风风场的移动有一定的延迟性，降温会持续较长时间。
模拟海表温度与 OISST V2.0 卫星数据的对比
本文选择美国国家海洋和大气管理局（NOAA）的 OISST V2.0 海表温度卫星数据进行验证。空间分辨率为 $0.25^\circ \times 0.25^\circ$，该产品中的 AMSR + AVHRR 数据是通过 AMSR 微波反演得到的，适用于台风过程的温度验证。选取 UTC2014-07-17_06:00:00（模拟 24h），UTC2014-07-18_01:00:00（模拟 43h）两个时刻进行验证，结果如图 7 所示。
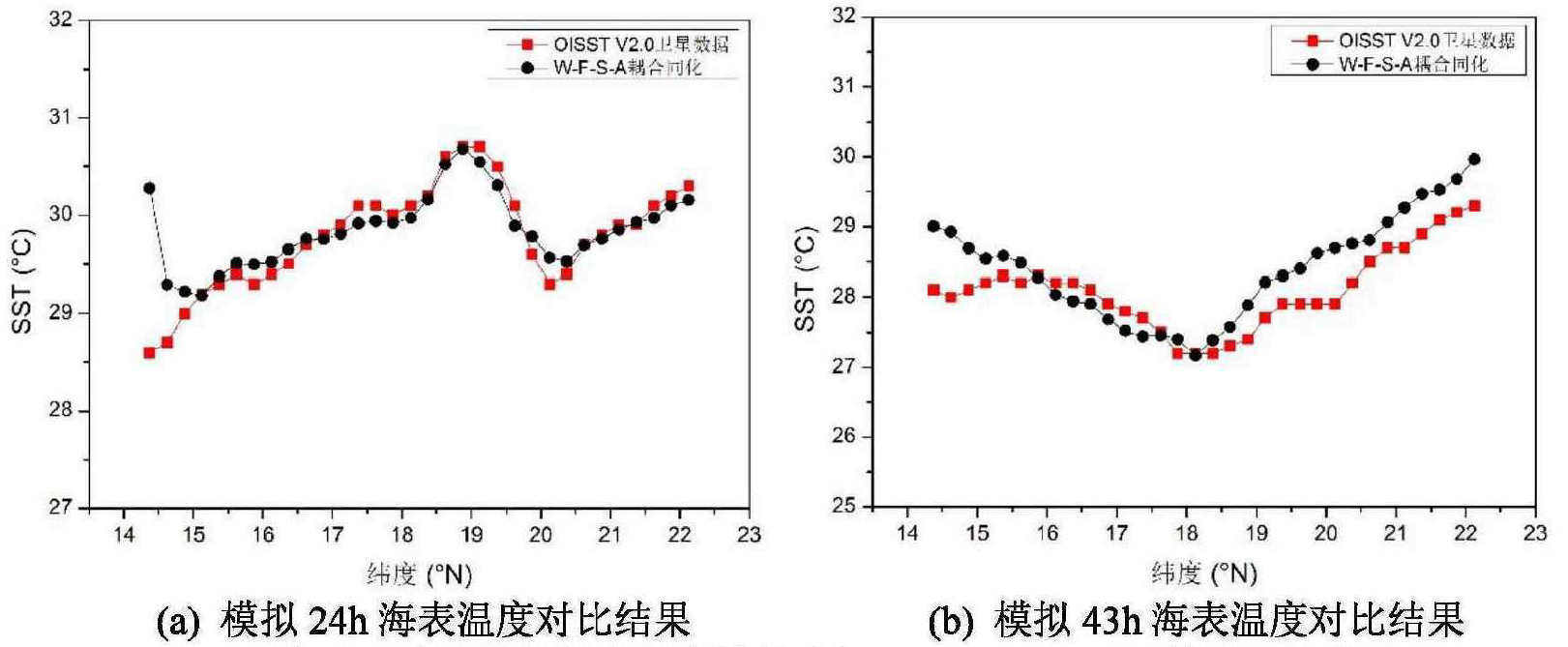图 7. 台风“威马逊”海表温度模拟值与 OISST V2.0 卫星数据对比结果
可以看出，模拟结果与卫星数据吻合较好，趋势一致，说明了 W-F-S-A 耦合同行模式的合理性。同时，从时间对比上看，模拟 43h 时台风发展已经较为强烈，整体温度明显低于 24h，印证了台风过程中海表温度降低的现象；从空间对比上看，模拟 43h 时台风中心在北纬 $18.4^\circ$ 附近，可以看出此处 SST 明显低于周围。
本章小结
本章首先对 201409 号台风“威马逊”的流场特征、温度场特征进行了分析，说明了 W-F-S-A 耦合同化模式能较好地反映出台风过境时海表温度下降的现象。并将 W-F-S-A 耦合同行模式模拟得到的 SST 结果与 OISST V2.0 卫星数据进行验证，吻合程度较好。
台风过程的波浪场模拟
台风过程波浪场特征
台风过境海域时，最明显最剧烈的现象之一就是海表面产生的大浪，据前人研究成果，在台风风场作用下，台风路径附近海域会形成风场驱动下的波浪场。
本文以 201117号台风“纳莎”为例，说明台风作用下的波浪场特征。感兴趣者请移步原文
由有效波高等值线的分析可得出，台风下的波浪场有以下特征：1. 波浪场中心为小浪区，中心四周波浪较大；2. 波浪场中心位于台风中心左后方，可见波浪对台风的响应作用有一定的延迟；3. 在台风登陆前，波浪场的大浪区基本位于台风路径的右侧，并且各时刻有效波高最大值也基本出现在台风移动方向的右前方，因此台风下的波浪场具有明显的右偏性。
模拟结果与卫星高度计资料的对比
卫星高度计资料的选取
对台风过程波浪场数值模拟的结果除了分析波浪场特征外，还需要通过与实测资料的对比验证分析模拟误差，本文实测验证数据采用 AVISO 发布的 OSTM/Jason-2 卫星高度计数据。Jason-2卫星有三种数据类型，分别为 OGDR、IGDR、GDR，其中 GDR 数据有三种格式的数据，本文采用最复杂的 S-GDR 数据集，其为专业的传感器产品，包括了所有的雷达回波信息。
Jason-2 卫星的扫描轨迹是具有周期性的，经过绘图发现，第 153 条扫描轨迹恰好经过南海，卫星地面轨迹如图 8 所示。值得注意的是，Jason-2 卫星是按照一定的时间间隔经过南海上空，因此其经过南海时不一定有台风发生，换言之，不能保证每一场台风过程下的波浪场都有相应的卫星数据进行验证，从另一个方面来说，70 场台风采用的地形参数、物理参数、耦合参数、同化方案都是一致的，因此采取抽样调查的思路，只需要验证一定数量的波高模拟结果，就可以基本说明所有模拟结果的合理性。
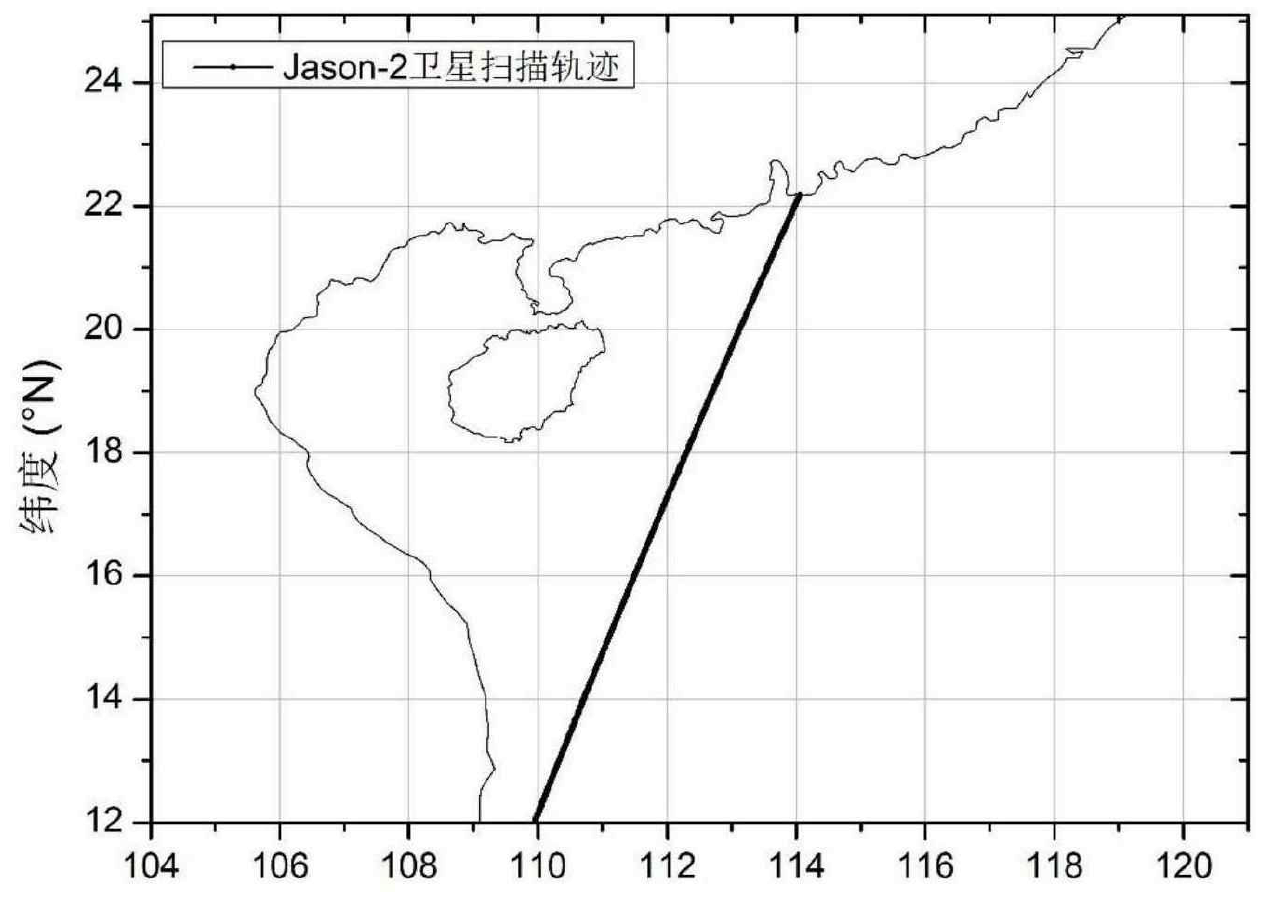图 8. Jason-2 卫星经过南海上空轨迹
验证-对照实验的设置和结果
关于本文采用的 W-F-S-A 耦合同化模型与 WRF 模型的实验对比与分析，请移步原文。
综合原文试验分析，说明 W-F-S-A 耦合同化模式模拟得到的波高结果是合理的，可以作为后续波浪要素推算的数据基础。此外，通过与纯 WRF 模式的对照，反映了耦合同化模式建立海表面粗糙度与波浪参数的关系的合理性，说明了耦合同化模式在模拟台风过程波浪场方面较 WRF 驱动 SWAN 模式更优，能反映出台风过程中海表面粗糙度的变化，更接近实际情况。
研究波向的确定及有效波高、平均周期的计算结果
对70场热带气旋的波向计算结果进行处理，按 N、NE、E、SE、S、SW、W、NW 进行 8 个方向划分，统计所有计算结果在各测点的波向频率结果，从而确定 8 个测点的研究波向。统计结果见表 5，研究波向确定结果见表 6，70场热带气旋的有效波高结果请移步原文，参见附录B。
表 5. 台风期间波向分布统计表
| N | NE | E | SE | S | SW | W | |
|---|---|---|---|---|---|---|---|
| 1号测点 | 16% | 39% | 13% | 6% | 8% | 4% | 7% |
| 2号测点 | 39% | 11% | 9% | 5% | 14% | 7% | 7% |
| 3号测点 | 9% | 9% | 14% | 30% | 12% | 12% | 6% |
| 4号测点 | 4% | 16% | 40% | 12% | 14% | 7% | 3% |
| 5号测点 | 9% | 43% | 14% | 13% | 11% | 5% | 3% |
| 6号测点 | 5% | 46% | 10% | 18% | 15% | 3% | 2% |
| 7号测点 | 9% | 48% | 19% | 10% | 4% | 2% | 3% |
| 8号测点 | 12% | 54% | 15% | 4% | 3% | 3% | 5% |
表 6. 8个测点研究波向的确定
| 测点 | 方向 | 测点 | 方向 |
|---|---|---|---|
| 1号测点 | NE | 5号测点 | NE |
| 2号测点 | N | 6号测点 | NE |
| 3号测点 | SE | 7号测点 | NE |
| 4号测点 | E | 8号测点 | NE |
本章小结
本章首先对 201117 号台风“纳莎”的波浪场特征进行了分析，并将 W-F-S-A 耦合同行模式模拟得到的波高结果与 Jason-2 卫星高度计数据进行验证，吻合程度较好。同时设置了 6 组耦合同化模式与 WRF 驱动 SWAN 模式的对照试验，说明了耦合同化模式较单一模式更能反映出台风过程中海表面粗糙度的变化，与实际情况更相符。最后对所有的有效波高、平均周期、波向结果进行数据处理，确定了 8 个测点的研究波向，统计出 70 场 热带气旋过程中的最大有效波高结果、最大平均周期结果。
不同重现期设计要素推算
极值推算方法
年最大值分析法
目前不同重现期设计要素的推算普遍采用年最大值分析法，就是对所分析要素按照每年的最大值取值，得到一组年最大值序列，再选配一条合适的理论频率曲线，外延推求多年一遇设计波高。应用于水文频率统计的概率分布函数主要有皮尔逊 III 型分布、对数正态分布、耿贝尔第一型极值分布和威布尔分布等。
皮尔逊 III 型分布
皮尔逊 III 型分布曲线（P-III 型分布曲线）是我国《港口与航道水文规范》（JTS145-2015）中推荐的波高分布曲线，国内经验表面，它对于年最大值有效波高及其对应的平均周期的理论频率曲线拟合较好，年最大风速和河流的洪水频率的分析中通常也采用此种线型。对 P-III 型概率分布参数的取值，在水文频率计算中是十分重要的，因此，很多研究者一直致力于此方面的研究。目前，常用的参数估计方法主要有权函数法、极大似然法、适线法、概率权重矩法、线性矩法及常规矩法等。
耿贝尔分布
耿贝尔分布（Gumbel 分布）对水文气象极值计算有较大的适用性，只要随机变量的原始分布属于正态分布或 $\Gamma$ 分布等指数分布族，其极值分布就渐进于 Gumbel 分布。
本文对于不同重现期风速、不同重现期波浪平均周期额推算均采用年最大值分析法，其中对于不同重现期风速的概率分布函数选用 P-III 型分布，对于不同重现期波浪平均周期的概率分布函数选用 Gumbel 第一型极值分布。得到样本数据后进行初步分析处理，对于某个测点的设计要素系列，将设计要素按从大到小的次序排列，排序编号记为 $m$，再将 $m$ 代入式 22 计算其经验累积频率 $P$。
$$
P = \frac{m}{n+1} \times 100%
\tag{22}
$$
公式 23 拟推算设计要素的均值 $\bar{X}$。公式 24 计算波高的均方差 $S$。
$$
\bar{X} = \frac{1}{n}\sum^n_{i=1}X_i
\tag{23}
$$
$$
s = \sqrt{\frac{1}{n}\sum^n_{i=1} X_i^2 - (\frac{1}{n}\sum^n_{i=1} X_i)^2}
\tag{24}
$$
泊松-耿贝尔复合极值分布
泊松-耿贝尔复合极值分布是由马逢时等提出的一种利用极值分布理论（Gumbel 分布）推算海洋工程中设计波高的新方法。该方法的原理是，首先根据台风统计资料，经过分析得出影响某一个海域的台风发生频次极好的符合泊松（Poisson）分布；然后检验每次台风影响下形成的波高，得到波高分布在鲍威尔几率格纸上呈现直线关系，说明台风波浪波高原始分布符合耿贝尔（Gumbel）分布，由此形成了泊松-耿贝尔复合极值分布。《港口与航道水文规范》（JTS145-2015）中规定，对于台风多发海域，某一波向一年中出现一个以上较大台风波高时，可按台风波高的最大值系列取样，采用泊松-耿贝尔复合极值分布确定不同重现期的设计波高。因此，本文对于不同重现期波高的推算采用泊松-耿贝尔复合极值分布。
对于某一海域，假设台风每年在其附近经过并产生影响的次数为 $n$ 次，显然 $n$ 是一个随机变量它的分布函数应该符合某种离散型分布，$n$ 的取值范围为 $0~k$ 之间的整数，其相应概率为 $P_K$。每年每次台风在该海域形成的最大波高记为 $\zeta_i$，$i = 1 ~ n$。每年 $n$ 场台风浪中有一个极大值记为 $\zeta_n = \underset{1 \leq i \leq n}{max} {\zeta_i}$，设 $\zeta_i$ 的原始分布函数为 $G(x)$。当台风出现次数为 $n$ 时概率分布函数为 $P_K$ 的情况下，台风波浪的年极值 $\zeta_n$ 的分布函数 $F(x)$。根据概率的加法和乘法定理，$F(x)$ 可写为：
$$
F(x) = P \{\zeta < x \} = \sum_{k=0}^{\infty} P \{\zeta < x, n=k \} \\
=\sum_{k=0}^{\infty} P \{\zeta < x|_{n=k} \} P \{n=k \} \\
=\sum_{k=0}^{\infty} P \{max[\zeta_i] < x \} \cdot P_k \\
=\sum_{k=0}^{\infty} P_k \cdot [G(x)]^k
$$
由上式可见 $F(x)$ 是由 $n$ 的概率分布与 $\zeta$ 的概率分布两种分布所构成，所以称为复合极值分布。
经过我国沿海一些台风观测站的检验，每年台风出现的次数 $n$ 符合泊松（Poisson）分布，即
$$
P_k = e^{-\lambda} \frac{\lambda^k}{k!}
\tag{26}
$$
式中：$\lambda$ 为每年台风出现的平均次数，可按下式计算
$$
\lambda = 台风影响本海域总次数 / 总年数
$$
而台风波浪的经验累积频率点在鲍威尔概率格纸上近似成一条直线分布，说明台风波浪的分布耿贝尔分布，即：
$$
G(x) = e^ {-e^ {-x}} = exp \{-exp[-\alpha(H-u)] \}
\tag{27}
$$
式中：$\alpha$ 和 $u$ 为耿贝尔分布的两个参数，于是：
$$
F(x) = \sum_{k=0}^{\infty} e ^{-\lambda} \frac{\lambda^k}{k!} [G(x)]^k = e^{-\lambda[1-G(x)]} = 1 - P
\tag{28}
$$
式中：$P$ 为超值累积频率，即重现期的倒数。
将 $G(x)$ 的表达式代入上式得
$$
1 - Px_p = - ln \{-ln[1+\frac{ln(1-p)}{\lambda}] \} = \alpha(H_P - u)
\tag{29}
$$
$\alpha$ 与 $u$ 可通过全部台风波浪最大波高组成的系列的均值 $\bar{H}$ 及均方差 $S$ 计算，或用最小二乘法求解，它们与 $\bar{H}$ 及 $S$ 的关系为：
$$
\alpha = \sigma_n / S \\
u = \bar{H} - \frac{y_n}{\alpha}
\tag{30}
$$
式中：$y_n$ 与 $\sigma_n$ 为仅与 $n$ 有关的参数。
于是台风影响下，多年一遇的设计波高可按下式计算：
$$
H_P = u + \frac{x_p}{\alpha} = -ln \{-ln[1 + \frac{ln(1-p)}{\lambda}] \} \cdot \frac{1}{\alpha} + u
\tag{31}
$$
设 $N$ 年共出现 $n$ 次台风，并将 $\alpha$ 与 $u$ 的表达式代入，可得：
$$
H_P = \bar{H} + \beta S
\tag{32}
$$
式中：
$$
\beta = -\frac{1}{\sigma_n} \{y_n + ln[-ln(1 + \frac{N ln(1-p)}{n})]\}
\tag{33}
$$
传统方法对于不同重现期设计要素的推算
不同重现期风速的推算结果
对 W-F-S-A 耦合同化模式模拟得到的最大风速样本数据进行初步分析，将年最大风速从大到小进行排列，若某年发生的所有的热带气旋在某测点的最大风速模拟值均小于 $5m/s$，则认为该年份热带气旋对该测点的影响较小，不列入年最大风速序列。1-8 号测点的年最大风速序列表请移步原文。
不同重现期最大风速的推算采用的是P-III型分布，1~8 号测点的拟合曲线结果图请移步原文。8个测点重现期为 50年、20年、10年和 5年的风速推算结果请移步原文。
不同重现期波高的推算结果
具体请移步原文
不同重现期波浪平均周期的推算结果
具体请移步原文
风浪联合分布
联合概率方法简介
在台风过程中，需要推算的设计要素由最大风速、最大波高，水文频率分析的传统方法就是按照各要素的样本序列分别取值进行推算，各要素间是独立的。但实际情况是，最大风速、最大波高这两者一般不会出现在同一时刻，并且他们的组合形式是多样的，组合规律是复杂的。因此传统方法没有很好地体现出最大风速、最大波高这两者之间的关系，本文采用风-浪联合概率分布改善这一缺点。
联合概率分析方法取其中一种要素（如波高）达到最大值时与其同一时间出现的其他各要素（如风速等）的计算值，共同分别作为统计样本，如此一来，实现了最大风速、最大波高出现在同一时刻，然后将联合分布的样本按照各要素分别取最大值序列，采用相应的频率分析方法进行不同重现期设计要素的推算，拟合出各设计要素的频率分布曲线。这样就可以推算出不同重现期的分别以风速为主或以波高为主的各种极端设计要素组合情况。然后在结构设计时，选择对结构产生最大作用效应的组合作为环境极端条件。本文以有效波高为主要作用，推算在有效波高达到最大值时的联合分布频率，以此为例来分析联合分布与传统方法的区别。最大风速的理论频率曲线的选取和参数计算同传统方法。
联合分布样本数据
对 W-F-S-A 耦合同化模式模拟得到的风速和波高样本数据处理，对最大波高时刻对应的风速进行取值，得到的联合分布样本数据，请移步原文附录 D。
不同重现期风速的联合分布推算结果
不同重现期最大风速的联合分布推算采用的是 P-III 型分布，1~8 号测点的拟合曲线结果，请移步原文附录 E。
8个测点重现期为 50年、20年、10年和 5年的风速推算结果见表 7。
表 7. 各测点不同重现期风速联合分布推算结果 $(m/s)$
| 测点 | 方向 | 50年（V2%） | 20年（V5%） | 10年（V10%） | 5年（V20%） |
|---|---|---|---|---|---|
| 1号测点 | NE | 38.11 | 34.70 | 30.72 | 26.90 |
| 2号测点 | NW | 20.23 | 18.55 | 16.95 | 14.80 |
| 3号测点 | N | 38.00 | 32.10 | 27.60 | 21.20 |
| 4号测点 | NE | 53.83 | 46.93 | 41.18 | 34.70 |
| 5号测点 | NE | 50.40 | 43.91 | 38.53 | 32.18 |
| 6号测点 | NE | 41.23 | 36.99 | 33.36 | 28.14 |
| 7号测点 | NE | 46.42 | 41.26 | 36.52 | 32.34 |
| 8号测点 | NE | 43.43 | 39.41 | 35.84 | 31.52 |
联合分布与传统方法的比较
为了更好地说明联合分布与传统方法在推算设计要素方面的区别，将两者的计算结果进行比较。本文所采用的联合分布概率方法，选取有效波高为主要作用，因此波高的联合分布样本数据与传统方法的样本数据一致，其推算结果也一致。而最大风速的联合分布样本数据与传统方法的不同，风速推算的对比结果，请移步原文。
对比分析可得，传统的频率分析方法推算的设计要素较联合分布要大，是偏于保守的。此外，联合分布的方法以有效波高作为主要作用，其设计要素中的最大风速是与有效波高同时发生的，更加符合实际情况，在保证设计安全的情况下降低了工程的造价。
本章小结
本章分别采用传统方法和联合分布对不同重现期的风速、有效波高、平均周期进行了推算。其中对于不同重现期风速、波浪平均周期的推算采用年最大值法，对于不同重现期风速的概率分布函数采用 P-III 型分布，对于波浪平均周期的概率分布函数选用耿贝尔第一型极值分布。对于不同重现期波高的推算采用泊松-耿贝尔复合极值分布。
联合分布采用以有效波高为主要作用，推算在有效波高达到最大值时的风速的联合分布频率，并与传统方法进行对比，结果表明联合分布的推算结果较传统方法的设计标准均有所降低，说明传统方法偏于保守，联合分布更加符合实际海况，在保证设计安全的情况下降低了工程的造价。
结论和建议
结论
本文主要结论，不在此赘述，请移步原文
建议
大气-海洋-海浪的数值模拟是一个复杂的过程，由于时间限制，本文有些问题未进行考虑，在现有工作的基础上，以后可以进一步深入研究，本文提出一下几点建议，主要包括：
-
本文建立的大气-海洋-海浪耦合同化模式中，WRF 采用结构化网格，FVCOM 海洋模式和 SWAN 海浪模式采用了相同的非结构化网格，在 WRF 模式和其他两种模式传递数据的过程中需要进行插值，本文未考虑插值过程数值误差问题，后续需进一步研究。
-
本文波浪场外海边界波浪要素由更大的 SWAN 模式计算所得，SWAN 模式在深海计算结果可能逊于 WAVEWATCH，后续考虑采用 WAVEWATCH 模拟波浪场。
-
本文采用 泊松-耿贝尔复合极值分布，推算不同重现期的有效波高时，对于特大值的处理不够完善，导致部分特大值与曲线有一定的偏离，后续可以采用水文频率分析中对于特大值的处理方法进行调整。
-
本文的数据集采集方面注重了风、浪的同步性，但在进行联合分布时，若能够将多元极值理论应用进来，将达到真正的联合分布。
-
由于时间所限，本文处理了 20 年的风场资料进行重现期推算，严格意义上无法推算 100 年重现期的设计要素，后续可以增加风场资料至30年的数据，可以推算 100 年重现期，使结果更加完善。
[1]. 毛卿任. 台风过程的大气-海洋-海浪耦合与卫星数据同化模拟[D].天津大学,2019.
